Se lhe pedir para calcular 15 x 238 sem utilizar calculadora, o mais provável é que recorra ao algoritmo que lhe ensinaram na escola e que está representado na figura seguinte:
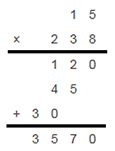
Apesar de este ser o mais utilizado na actualidade, ao longo da história da humanidade e em diferentes civilizações, muitos outros algoritmos foram utilizados para realizar multiplicações.
O mais antigo algoritmo conhecido para a multiplicação foi já alvo da nossa atenção no artigo “Matemática no tempo dos faraós”, publicado aqui em Novembro de 2015. Fruto do conhecimento disponível no Antigo Egipto, esse algoritmo recorria a duplicações sucessivas que lhes permitiam contornar as limitações que o seu sistema de numeração não posicional lhes colocava.
O salto civilizacional conseguido pela civilização Hindu, no séc. V a.C., com a introdução do sistema de numeração posicional de base decimal, permitiu a utilização de diferentes algoritmos, um dos quais chegou à Europa, no século XIII, pela mão de Leonardo Fibonacci (de quem já falámos anteriormente, no artigo “Coelhos, Girassóis e o Código Da Vinci”). Este algoritmo da multiplicação, conhecido como Método da Gelosia, assenta numa grelha onde se representam os números a multiplicar.
O uso do Método de Gelosia é muito simples e pode ser resumido nos 4 passos que apresentamos a seguir. Como exemplo, de como se multiplica usando o Método da Gelosia, vamos calcular 15 x 238.
Passo 1: Colocar os números a multiplicar, no top e no lado direito da grelha

Passo 2: Realizar a multiplicação referente a cada célula.
Para a primeira célula, calcula-se 2 x 1, O resultado obtido coloca-se nos espaços acima e abaixo da diagonal da célula, ficando o algarismo das dezenas em cima e o das unidade em baixo. Neste caso o resultado é 2, pelo que se coloca 02.

Na célula seguinte, deverá ser apresentado o resultado de 2 x 5, ou seja 10 (algarismo 1 nas dezenas e algarismo 0 nas unidades)
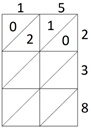
Continuando com as restantes multiplicações, 3 x 1 = 03 , 3 x 5 = 15, 8 x 1 = 08 e 8 x 5 = 40

Passo 3: Realizar as adições dos números que surgem em cada uma das diagonais.
Na primeira diagonal (a de baixo) só está um zero.

Na segunda diagonal surgem o 5, o 4 e o 8, calculando 5 + 4 + 8 o resultado é 17. Como só deve resultar um algarismo para cada diagonal, o algarismo das dezenas de 17, é transportado para a diagonal seguinte
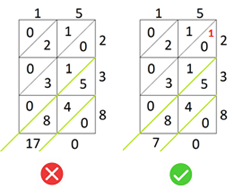
Na terceira diagonal, a adição será, portanto, 
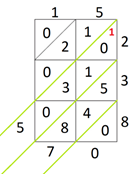
Na quarta diagonal, 1 + 2 + 0 = 3
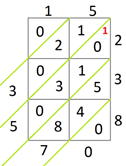
E na quinta diagonal, zero.
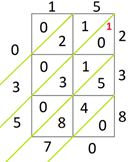
Passo 4: O resultado final da multiplicação é o número formado pelos algarismos que resultaram das diagonais, lidos a partir do superior esquerdo, para baixo e para a direita,

ou seja, 03570. O resultado é 3570.
Imagem de mountainsoftravelphotos.com