Medicina e Probabilidades

Em medicina, o sucesso de um diagnóstico passa, frequentemente, pela análise dos resultados fornecidos por testes diagnósticos médicos.

Recorrendo ao resultado do teste diagnóstico é possível transitar de uma probabilidade a priori (a prevalência da doença) para uma probabilidade a posteriori (após o teste) em relação à possibilidade de presença da doença, alteração que se pretende que conduza à redução da incerteza associada ao diagnóstico. A Teoria das Probabilidades, mais precisamente o teorema de Bayes, permite quantificar a referida alteração de probabilidade, com base na prevalência da doença e propriedades do teste.

Atendendo à impossibilidade de o resultado de um teste diagnóstico permitir afirmar, peremptoriamente, a presença ou ausência de doença, a escolha do teste a realizar e a decisão a tomar, com base no resultado de um teste, passa pelo conhecimento do poder que cada teste tem em detectar os enfermos e os sãos. Esta capacidade é traduzida pela sensibilidade e especificidade do teste.

A sensibilidade de um teste diagnóstico médico, que avalia a capacidade do teste detectar a doença quando ela está presente, fornece a probabilidade de, estando doente, ter um teste positivo. Testes de alta sensibilidade são importantes para o rastreio de doenças com implicações graves, em que é desaconselhada a presença de falsos negativos.

A especificidade de um teste diagnóstico médico, que avalia a capacidade do teste rejeitar a doença quando ela está ausente, fornece a probabilidade de, não estando doente, ter um teste negativo. Testes de alta especificidade são importantes para doenças em que o diagnóstico representa um impacto negativo na vida e pretensões do paciente, como, por exemplo, nos diagnósticos de cancro e SIDA.

Poderemos dizer que a sensibilidade e a especificidade representam as taxas de verdadeiros positivos e verdadeiros negativos, taxas que correspondem às situações em que o teste acerta. Em contraposição existem também duas situações em que o teste erra, cujas probabilidades de ocorrência são conhecidas como taxa de falsos-positivos e taxa de falsos-negativos. A primeira correspondendo à probabilidade de não estando doente, ter um teste positivo, e a segunda à probabilidade de estando doente, ter um teste negativo.

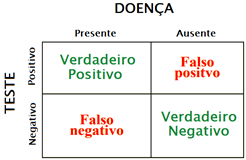
Os valores da sensibilidade e especificidade permitem avaliar o poder de um teste diagnóstico, contudo o cálculo destes valores tem como ponto de partida algo que se desconhece no momento em que o paciente faz o teste - o verdadeiro estado de saúde do paciente. Posto isto, a decisão do médico terá que ser tomada com base noutros valores, designados por valor preditivo positivo (VPP), que corresponde à probabilidade de um indivíduo cujo teste deu positivo, estar (de facto) doente, e valor preditivo negativo (VPN), que corresponde à probabilidade de um indivíduo cujo teste deu negativo, estar (de facto) são.

Do ponto de vista da Teoria das Probabilidades, os conceitos de sensibilidade, especificidade, VPP e VPN são probabilidades condicionadas.

A probabilidade condicionada é um dos pilares da tomada de decisão em diversas situações, mas constitui um desafio para a intuição humana, verificando-se uma enorme incidência de equívocos aquando da sua interpretação.

No caso das probabilidades condicionadas associadas às características do teste diagnóstico médico, a reduzida intuição probabilística do ser humano e a renúncia à Teoria das Probabilidades reflecte-se na dedução errada de que a sensibilidade e especificidade do teste coincidem com o VPP e o VPN, respectivamente. Esta confusão, designada por falácia da condicional transposta, vem sendo alvo de vasta investigação devido à sua elevada incidência e às graves repercussões que acarreta quando presente na tomada de decisão em áreas nevrálgicas  como a Medicina ou a Justiça.

Como ilustração, da diferença entre a sensibilidade de um teste diagnóstico e o seu valor preditivo positivo, consideremos um problema usado por um médido especialista em tomadas de decisão clínicas, David Eddy, num estudo sobre a complexidade da tomada de decisão médica e os equívocos na interpretação das probabilidades. Eddy solicitou aos participantes que estimassem a probabilidade de uma mulher, cuja mamografia deu positiva, ter realmente cancro da mama, ou seja, solicitou o VPP. A informação que fornecia era: a prevalência da doença (1%), a sensibilidade do teste/mamografia (80%) e a taxa de falsos-positivos do teste (9,6%).

Os resultados obtidos por Eddy confirmaram as suas suspeitas sobre a presença da falácia da condicional transposta, na interpretação das probabilidades associadas aos testes diagnóstico, verificando-se que a grande maioria dos participantes no estudo estimaram a probabilidade com um valor quase dez vezes superior à verdadeira probabilidade de a mulher, cuja mamografia deu positiva, ter cancro da mama.

Recorrendo ao Teorema de Bayes e apresentando os dados do problema num diagrama de árvore, calculamos o VPP, ou seja, a probabilidade de uma mulher, cuja mamografia deu positiva, ter realmente cancro da mama. Para facilitar a interpretação, os valores relativos aos dados do problema foram convertidos em frequências naturais, assumindo-se, para tal, um conjunto de 10000 mulheres.

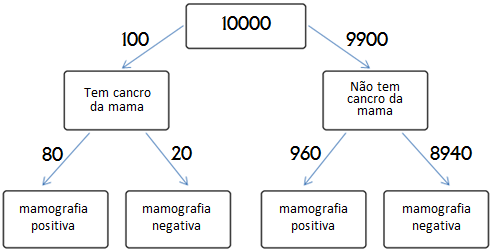
 Da observação do diagrama, verifica-se que, das 10000 mulheres, 1040 (80+960) têm uma mamografia positiva, mas que dessas 1040 mulheres apenas 80 têm cancro da mama. Assim, a probabilidade de uma mulher cuja mamografia foi positiva ter, de facto, cancro da mama é 80/1040, ou seja, menos de 8%.

Siga o Tribuna Alentejo no  e no . Junte-se ao Fórum Tribuna Alentejo e saiba tudo em primeira mão.